Learning from data, efficiently.

What is active learning?

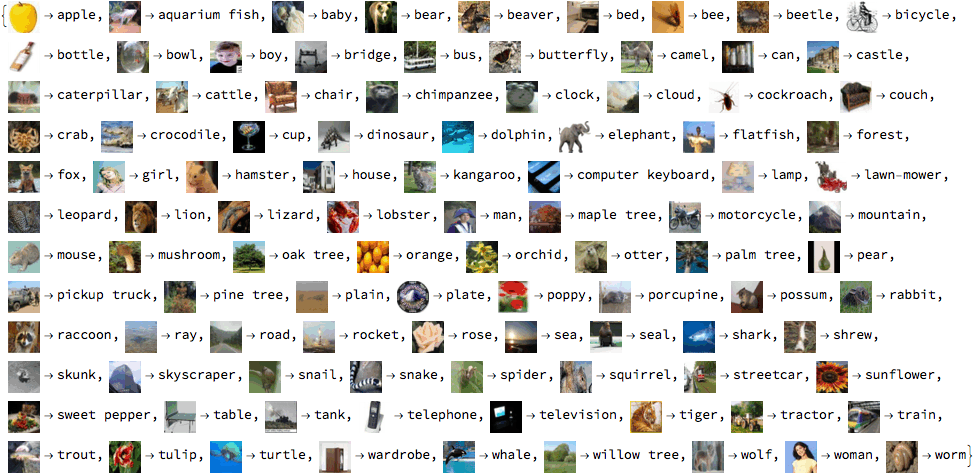
Deep learning (DL) rocks in domains with lots of data. Take image classification, for example. One popular dataset contains 60,000 colour images, each with one of 100 possible labels - see Figure 1 for examples¹. The task is to label the images correctly, and our current best model can do so with 93% accuracy.

Figure 1: labelled images in the CIFAR-100 dataset

Hence the slogan “data is the new oil”: if you’ve got lots of data about some problem, there’s a good chance you could train a DL model to solve it. (Though keep in mind that we’re only talking about problems that are “well-defined” in the mathematical sense, like “labelling images”, “winning at a game” or “guessing the next word in a sentence”.)

But suppose you wanted to use DL to, say, detect a rare cancer from a medical scan. For such problems where data is costly to obtain, current methods don’t get you too far.

How do humans learn to solve problems when it’s costly to obtain training data? Well, it seems that one thing we do is seek data on the parts of the problem that would be the most informative. This allows us to learn efficiently. Basic example: a few days ago I was learning how to play a new board game. In one situation in particular, I kept getting confused about which moves I could take. So to get the most information about how I could play better, I asked for clarification about the possible moves in that situation.

We’d like our DL models to do the same, so we can apply them in domains where it’s costly to acquire data.

And that’s what active learning is. More precisely, it’s a framework for training a model to a particular accuracy while minimising the need for labelled data. For instance, in image classification, that means training a model that labels images from some dataset, to a particular accuracy (e.g. 90%), while minimising the number of times the model needs to ask some human to label an image in the dataset.

Okay, so how do you do that?

The key idea is to ask the human to label only the most informative images. So, what we need is a method for measuring the informativeness of different datapoints. Then you use that method to select the most informative points, until your model has achieved the desired accuracy².

That method is called an acquisition function. Given a model and a datapoint (e.g. an image), it quantifies how informative the label of that datapoint (e.g. “apple”) would be to the model. In other words, it quantifies how much that label would help the model to solve whatever problem it’s solving with higher accuracy. It’s called an “acquisition function” because “acqusition” is the technical term for “the model asking the human to label a datapoint” - it “acquires” a new point for the training data.

Going back to our image classifier from earlier, suppose that it’s currently very good at distinguishing between different vehicles, but gets confused when distinguishing between different flowers. A well designed acquisition function would give low scores to images of vehicles, and high scores to images of flowers. Flowers are more informative than vehicles, because the model has already learned how to distinguish vehicles from one another, but hasn’t for flowers. The acquisition function tells the model where it has the most room for improvement.

In the rest of this post, I’ll explain four popular acquisition functions and give intuitions for their advantages and disadvantages. Interestingly, there isn’t yet a consensus view on which of these functions is the best. Keep in mind during the discussion that deep learning is an empirical field; we can argue however much we like about the merits of different functions, but ultimately rely on papers like these to evaluate them in practice.

A running example

To illustrate the intuitions behind different acquisition functions, it’ll help to have an example we return to. Let’s take our image of an apple, and pretend for simplicity that instead of 100 possible labels in the dataset, there are only two - apple or orange (extending to more labels doesn’t change the underlying intuitions, it just makes them a bit harder to grasp). So the task is: given an image, decide whether it’s an apple or an orange. Our DL model will actually output probabilities - how likely is the image to be an apple, p(apple), or an orange, p(orange). Since there are only two possible labels, p(apple) + p(orange) = 1.

Finally, we’ll need a little bit of jargon. We have a large dataset of unlabelled images of apples and oranges, called the pool data. Using our acquisition function, we find the most informative image, ask a human to label it (as either an apple or an orange), and then add the labelled image to our training data. The model is then trained on this data (using standard deep learning techniques), and the process repeated. As explained above, the active learning problem is (in this case) to train our model to a certain level of accuracy at distinguishing apples from oranges, whilst minimising the number of times we need to ask a human to label an image from the pool data.

Warm up

As a warm up, one basic idea could be to acquire an image of the fruit that is currently the most underrepresented. Let’s say that our current training data consists of 5 apples and 2 oranges. It might be reasonable to guess that our model could do with some more information about the underrepresented oranges. So our acquisition function would find the image in the pool data that it thinks is most likely to be orange, i.e. for which it outputs the highest p(orange) value.

There are (at least) two problems with this idea. Firstly, if “apple” is somehow a harder concept to learn than “orange” (e.g. because apples come in many colours, but oranges are mostly orange), the model might actually need to acquire more apple images even if they’re overrepresented. Secondly, acquiring only oranges with the highest p(orange) values might not be a good strategy. Since the model is already very certain that these images are oranges, they are likely to be very “clear cases” of oranges. And so if the model is only trained on these very “orange-y” oranges, it is unlikely to perform well when tested on more confusing orange images (e.g. an unripe orange that is a bit green).

Nonetheless, hopefully this starts to build some intuition of what we’d like to see in a good acquisition function. So now let’s discuss some acquisition functions currently used in deep learning.

Variation ratios

You can think of this first acquisition function as an attempt to solve the second problem with our warm up function. It acquires the image about which the current model is the most uncertain/confused, i.e. on which its predictions for p(apple) and p(orange) are the closest to 0.5.

For the mathematically inclined, this is formalised as:

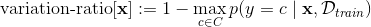
for input (image) with label in possible labels , and training data .

It turns out that this simple idea actually works pretty well. In particular, it doesn’t acquire only oranges with the highest p(orange) values, like our warm up function (which I argued was a bad idea). However, it’s prone to a subtle failure mode. To see what that is, we need to consider a DL model that accounts for uncertainty in its predictions in a slightly more sophisticated way. This model can make repeated predictions about the label of the same image, and these predictions may be different (our earlier model would output the same predictions every time if queried multiple times). This might sound a bit strange - surely we prefer models that “make up their minds” and don’t give different predictions for the same image? However, consider that when humans try to answer complex questions, we tend to use different methods, each of which give different answers, then we try to aggregate those answers in a sensible way. The model I’m describing is kind of the deep learning equivalent of that³. And it aggregates the predictions made by different “methods” by averaging them.

So, suppose we use this new model to make multiple predictions about some image. Let’s imagine, for this first image, it outputs “p(apple) = 0.5, 0.5, 0.5, …” every time. That is, no matter which “method” it uses, it’s always maximally confused about whether the image is an apple or an orange. In this case, it’d be reasonable to assume that the image is just inherently ambiguous. It’s probably a low quality image with lots of noise, and finding out its “true” label will probably not help improve prediction accuracy on the majority of images in the dataset (which aren’t so noisy). In some sense, this uncertainty is “irreducible”: it can’t be resolved given more data. We call this type of uncertainty aleatoric uncertainty⁴.

Now, suppose we have a second image, on which it outputs “p(apple) = 0, 1, 0, 1, …” and so on. When applying a particular method, the prediction has high confidence, but there is large disagreement between predictions made using different methods. In other words, the uncertainty is about which method is correct. So, acquiring this image gives an opportunity to work out which methods are right and which are wrong (which is probably valuable information for the model). We say these kind of inputs have high epistemic uncertainty⁵ (also known as model uncertainty).

To bring these examples together, the final thing to notice is that the variation ratios acquisition function wouldn’t be able to distinguish between these two examples. Since the model simply averages the predictions made by different methods, it outputs p(apple) = 0.5 as a final answer for both images, and so variation ratios would score the informativeness of the images equally - not the right thing to do.

Instead, we need an acquisition function that looks into the predictions made by the model’s different “methods”, before averaging takes place, and acquires data with high epistemic but low aleatoric uncertainty. The next function, mean standard deviation, is an attempt to do just that.

Mean standard deviation

The key insight of mean standard deviation is the following: images for which the model’s different predictions have high standard deviation - meaning they are very spread from their average value - tend to have high epistemic but low aleatoric uncertainty. For instance, taking the examples above:

• For both images, the average prediction is 0.5.
• For image 1, on which the model outputs “p(apple) = 0.5, 0.5, 0.5, …”, the predictions are all equal to their average value, so the standard deviation is 0.
• For image 2, on which it outputs “p(apple) = 0, 1, 0, 1, …”, the predictions each deviate by 0.5 from their average value, so the standard deviation is 0.5.

Therefore, to acquire data of high epistemic but low aleatoric uncertainty (and in particular acquire image 2 instead of image 1), we’d like our acquisition function to: generate a sample of predictions for each image, compute the standard deviation of each sample, and acquire the images for which that standard devaiation is the highest. And this is exactly what mean standard deviation does.

For some reason, this function doesn’t always work well in practice (finding out why is an open research question)⁶. However, our final function, which builds on the same intuition of acquiring data with high epistemic and low aleatoric uncertainty, but has a more rigorous justification in information theory, takes the cake.

Directly quantifying epistemic uncertainty

The final idea is to borrow some fancy maths from information theory to quantify epistemic uncertainty directly, instead of approximating it via the mean standard deviation of the predictions. The main concept we’ll need is entropy (which is analogous to entropy in thermodynamics). Intuitively, it represents the amount of uncertainty in a random variable’s possible outcomes. In our example, that means the amount of uncertainty in our model’s predictions about an image’s label, and the definition is:

.

If that looks scary, let’s run through two examples. If the model outputs p(apple) = p(orange) = 0.5, then entropy = -(0.5 log(0.5) + 0.5 log(0.5)) ≈ 0.69, which is the maximum value it can take in this case. If the model outputs p(apple) = 0 and p(orange) = 1, then entropy = -(0log0 + 1log1) = 0, which is the minimum value it can take. For the intermediate values, take a look at this graph to see how the entropy varies. Hopefully, you can see how these values fit the intuitions that if the model predicts p(apple) = 0.5, it’s maximally uncertain, and if it predicts p(apple) = 0, it’s minimally uncertain (maximally certain it’s not an apple).

But you might now be wondering: do we calculate entropy before or after averaging the predictions made by the different “methods”? This turns out to be the key to applying our definition of entropy to compute both aleatoric and epistemic uncertainty.

Let’s revisit the example used in the sections above. Recall that for image 1, the model outputs “p(apple) = 0.5, 0.5, 0.5, …” and for image 2, it outputs “p(apple) = 0, 1, 0, 1, …”. If we calculate entropy after averaging the different predictions, we plug in p(apple) = 0.5 for both images, resulting in entropy = 0.69 for both images. So we end up in the same failure mode as variation ratios: being unable to distinguish between aleatoric and epistemic uncertainty. Because we applied the definition of entropy to the overall, aggregated prediction, we got the overall entropy, rather than either of its components.

If we calculate entropy before averaging the different predictions (that is, calculate the entropy of each prediction individually, then average them), we get 0.69 for image 1, but 0 for image 2 (since entropy is -(0log0 + 1log1) for every prediction). Magically, this is the aleatoric uncertainty - the irreducible uncertainty that is high when all the methods are confused due to the noise in the input, and can’t be resolved given more data. This actually makes sense if you think about it: by first calculating the entropies of the predictions made by each method individually, then averaging the entropies, we are essentially eliminating epistemic uncertainty in the entropy calculation (uncertainty about which method is correct), because each calculation uses the predictions made by one particular method.

To tie things together: entropy after averaging predictions gives us the overall uncertainty the model has about the image’s label, whereas entropy before averaging gives the aleatoric uncertainty. So, if we subtract aleatoric uncertainty from overall uncertainty, we’ll be left with epistemic uncertainty - which is what we wanted.

If you’re into the maths, this can be written as:

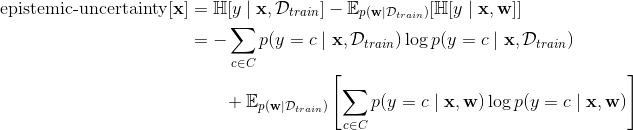
where is the entropy of a random variable and the expectation is over samples from a distribution over our model’s parameters (each sampled parameter represents what I’ve been referring to as a different “method”).

As a bonus for readers who know some information theory, there is an alternative way to arrive at the same result. Notice that the definition above corresponds to the mutual information between and - in other words, the information gained about , the model parameters, by observing , the image label - exactly what we wanted from our acquisition function.

Links to relevant literature

• The original paper which introduced active learning (1995).

• The book which introduced variation ratios (1965).

• Some papers which used mean standard deviation (2015, 2016).

• The paper which developed the idea of directly quanitfying epistemic uncertainty (2011).

• The first paper which successfully applied active learning in the case where the model is a deep neural network (2017), and compared the variation ratios, mean STD and BALD acquisition functions.

1. In case you were wondering, students were paid to undertake the thrilling task of labeling the 60,0000 images. ↩

2. This is a slight oversimplification; you also need to reinitialise and retrain your model after each acquisition. Also, if you acquire too many points in one shot, lots of them may be redundant, because they all help to resolve a similar uncertainty. A solution to the latter problem is proposed here. ↩

3. Okay, so this is a loose and intuitive explanation of what the DL model actually does. To be more precise, when I say it uses different “methods”, what it actually does is make different draws from its distribution over the model parameters. That’s right, unlike typical DL models which are parameterised by scalar weights, this model is parameterised by posterior distributions over each weight. In this setting, learning means updating these distributions given the new data, and making a prediction means drawing concrete, scalar parameters from these distributions and passing an input through the model with those concrete parameters. This is how the model makes multiple predictions for one input. What I’ve just described is called Bayesian deep learning (if you’re interested, here’s more about that). ↩

4. The name derives from the Latin aleator meaning ‘dice player’. The noise present in these inputs means that their labels are pretty random; they depend on the throw of a dice. ↩

5. The name derives from the Greek epistēmē meaning ‘knowledge’. These examples give an opportunity to acquire knowledge by resolving uncertainty about the correct method to use. ↩

6. E.g. see Figure 1 in this paper. ↩